Projectile Motion Paths in MatLab

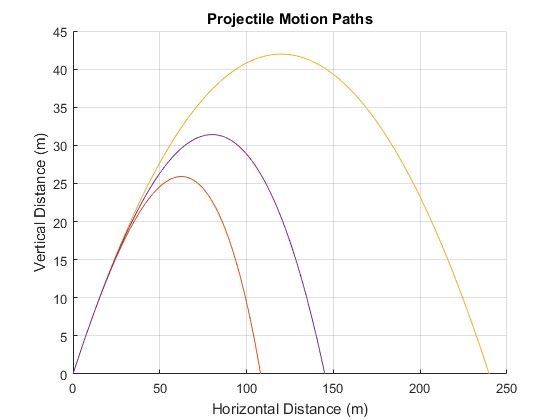
The following is a MATLAB script which produces the projectile paths of a spherical object, such as a cannonball, given radius (r), mass (m), initial velocity (v), and angle above the horizontal (theta). By changing the experimental variables mentioned above, and others attributed to the environment, such as the density of air (rho), gravity (g) and the drag coefficient (C) the various effects can be visualised in the graph this script outputs. 

ifr=1;

C=0; C1 = 0.5;

theta=35;   

v = 50;     

 

g= 9.80;    

dt = 0.0001; 

i = 1;

max_iters = 1000000;

x(1) = 0; y(1) = 0;

x1(1) = 0; y1(1) = 0;

t0 = 0;

while ifr<=2

    r=0.036*ifr;

    m=0.145*ifr^3;

    rho=1.2;

    

    A=pi*r^2; A1=pi*r^2;

    D=rho*C*A/2; D1=rho*C1*A1/2;

    

    vx =v*cosd(theta); vx1 =v*cosd(theta);

    vy =v*sind(theta); vy1 =v*sind(theta);

    

 while y(i) >= 0 && i < max_iters  

        ay=-g; ay1=-g-(D1/m)*(vx1^2+vy1^2)^0.5*vy1;

        ax=0.0; ax1=-(D1/m)*(vx1^2+vy1^2)^0.5*vx1;

        x(i+1)=x(i)+vx*dt+.5*ax*dt^2;

        y(i+1)=y(i)+vy*dt+.5*ay*dt^2;

        x1(i+1)=x1(i)+vx1*dt+.5*ax1*dt^2;

        y1(i+1)=y1(i)+vy1*dt+.5*ay1*dt^2;

        vx=vx; vx1=vx1+ax1*dt;

        vy=vy+ay*dt; vy1=vy1+ay1*dt;

        i=i+1;

 end

    

    t = 2*v*sin(theta)/g;

    tflight = 2*v*sin(theta)/g;

    ranged = v^2*sin(2*theta)/g;

    

    [maxYValue, indexAtMaxY] = max(y);

    [maxYValue1, indexAtMaxY1] = max(y1);

    xmax = x(indexAtMaxY(1));

    xmax1 = x1(indexAtMaxY1(1));

    disp(xmax*2);

    disp(xmax1*2);

    i=1;

    ifr = ifr+1;  

    

    xlabel('Horizontal Distance (m)');

    ylabel('Vertical Distance (m)');

    title('Projectile Motion Paths');

    axis([0 250 0 45]);

    grid on, hold on

    plot(x,y,x1,y1);  

end

The script as it is above produces the following graph:

𝑟 = 3.6 (𝑐𝑚) ∗ 𝑖𝑓𝑟
𝑚 = 0.145 (𝑘𝑔) ∗ 𝑖𝑓𝑟 3
𝑣 = 50 (𝑚/𝑠) 𝜃 = 35 (degrees above horizontal)
Orange line: C=0.5, ifr=1 (with air resistance)
Purple line: C=0.5, ifr=1 (with air resistance)
Yellow line: C=0, ifr = 1 OR 2 (without air resistance)